Untitled

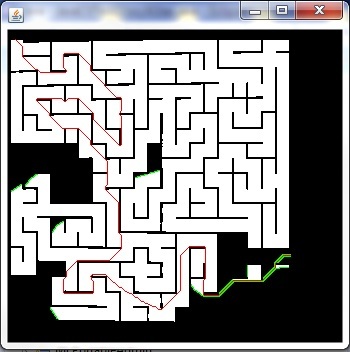
Well A* works amazingly, some concerns are:

1)It uses a lot of memory, not sure how well it will run on the android.

2)It’s not the fastest, takes a will to go through the entire maze on a desktop so I assume it will take far longer on the phone’s hardware

Fortunately I have a solution that should get rid of those issues.  Right not it really doesn’t need to scan through every single pixels, the only places on that map that really matter are intersections; where user has to make a decision on where to go.  If I can write a method (who knows how) that will get the center points of these intersections, the ammount of nodes will be reduced significantly from ~60000 elements in my closed list to around 20.

Also I previously mentioned using insertion sort, turns out O(n) with 60000 elements is not so good.  Binary heaps were the right answer with O(1) to get the smallest element and O(log n) to delete and insert.

Writing the code to get rid of this redundant information presents the largest challange, off the top of my head I’m thinking using houghlines and finding areas that are roughly the lanelength^2.  However code like that will only really be applicable to the rectangular maze case, if I ever want to generalize it to solve any maze I’ll have to come up with a better solution.

For now I think I will just get the rectangular case working flawlessly for any rectangular maze then go from there.